How To Find Frequency Count Of Algorithm
A Priori Analysis of Algorithms
Algorithm Assay — Role 3
Hello, and welcome dorsum to the Applied Guide to Algorithm Analysis.
This is Function 3 of the series, and I hope past this postal service, you will become to learn the central techniques to read and analyse simple iterative algorithms that doesn't exercise anything! Don't worry, we'll become to touch meaningful algorithms later in the series.
Also in this post, we'll get to bear upon some of the maths from the previous post –so be sure to become dorsum at that place when y'all feel you lot're lost in the maths.
So, the technique that I'one thousand going to teach you in this post is called frequency counting, which is a form of a priori analysis, and the goal is to count how frequently a line of code is executed. The basic thought is that the college the frequency (the higher the line needs execution), the longer time that a computer needs in order to complete the work.
As programmers, we aim to create programs which run fast, and consume as petty retention as possible. There are two properties that needs emphasis hither: time, and space — which leads to what you typically read in algorithm books as: the fourth dimension complexity and the space complexity. For at present as to give you a basic agreement, let's drop the complexity function of fourth dimension and space.
In gild for the program to run fast, it should perform lesser piece of work every bit possible. This is where frequency counting comes in. The higher the frequency count, the more than work that the computer needs to get done, the more time information technology takes for the computer to complete the work.
So, earlier we rush into the activeness, permit's commencement become familiar some of the basic concepts of frequency counting:
one. Any line of lawmaking that performs whatsoever operation, as long as the lawmaking isn't a function definition or a loop, is causeless to perform in constant time — counted as 1 execution.
2. Whatsoever user input are assumed to have an arbitrary size, and volition be represented by n. Any operation performed n times, either by a loop or a function, are counted as northward executions.
Okay ready?
At present, let's get downward to concern!
Consider the following snippet:
snippet1: (1) for i <- 1 to north:
(2) for j <- one to n:
(3) print(i,j)
Fancy that loop? Nope? Okay.
What we are interested in is to analyse the fourth dimension complexity of the snippet above to determine how well it performs (either fast or slow) — by counting the number of times each line executes (frequency count), and having an interpretation based on the number of times the entire loop is executed (Big-Oh).
Starting with line (1), for i <- i to north . How many times will this execute?
For beginners, if information technology'due south not quite obvious, we can rewrite the line equally:
(1) for (i=1; i<=northward; i++) // rewritten: for i <- 1 to n Starting from i=1, this loop volition execute n times.
Yet, at that place volition exist 1 more iteration which will evaluate i<=due north as false, thereby exiting the loop. So, the total number of executions is: n+ane.
Using the aforementioned technique we used to a higher place, line (2)for j <- 1 to n is evaluated to likewise have n+1 number of executions.
Nonetheless, notice that loop j in line (2) is nested within the loop i in line (ane)? So loop j will be repeated northward times.
In total: line (2) volition be executed (north+1)(north) times.
Line (3) is executed 1 time (equally per the basic concept #i indicated above). Notwithstanding, line 3 is written inside two nested loops, and must be evaluated accordingly. In total: line (3) will execute (i)(n)(n) times. The first n is from the inner loop j, and the second n is from the outer loop i.
In summary, the execution of each line is as follows:
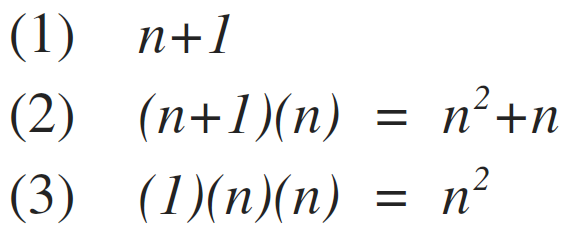
Which yields a sum of:
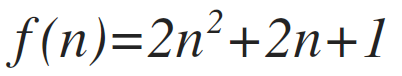
Every bit an estimate, snippet1 will have a worst-case operation of:
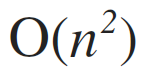
Never heard of Big-Oh earlier? Don't worry. It's non every bit scary equally information technology sounds. I will be covering BigOh, as well as other asymptotic notations, in the adjacent office of the series. For now, consider Big-Oh as the worst case estimation of the code.
At worst, the loop in snippet 1 volition behave northward-squared times given the size due north. Which means, if we have the size n=3, the loop is estimated to perform ix times. The Big-Oh of n-squared is likewise known as quadratic time — more than into these in the next part of the serial.
The offset ones easy! Okay, some other case:
snippet2: (i) for i <- 1 to n:
(2) for j <- 1 to i:
(3) print(i,j)
Line (one) is obviously n+1. Since i<=n is evaluated n times, plus the 1 last iteration that evaluates i<=n as faux, telling the loop to terminate.
Line (two) is a little bit tricky. If yous evaluated it equally (northward+1)(northward), you're incorrect. Notice that loop j is dependent non of n but of i. Even so, i is a variable which initially has a value of 1 to n. And then, to write an estimation, we need to write it in summation form as follows:
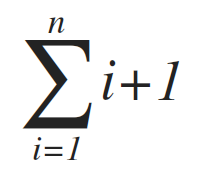
Yous may wonder why loop j is evaluated to exist the sum of i+1. The +1 refers to the ane iteration that evaluates j<=i as imitation, thereby exiting loop j.
Accept time to digest it, because we will be using some of the arithmetic series formulas from the mathematical preliminaries in function 2 of this serial.
We demand to determine the frequency count of line 2 where we can use it later to add with lines 1 and 3. In order to do so, nosotros need to simplify the summation equally follows:
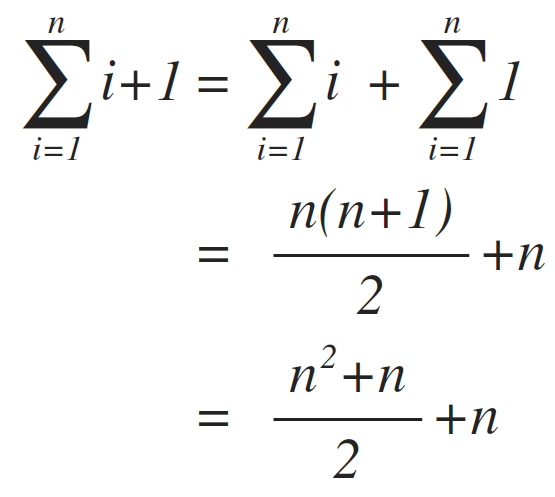
Using the techniques we learned so far, we tin can evaluate line (3), as follows:
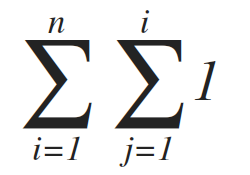
Which, if simplified, yields to:
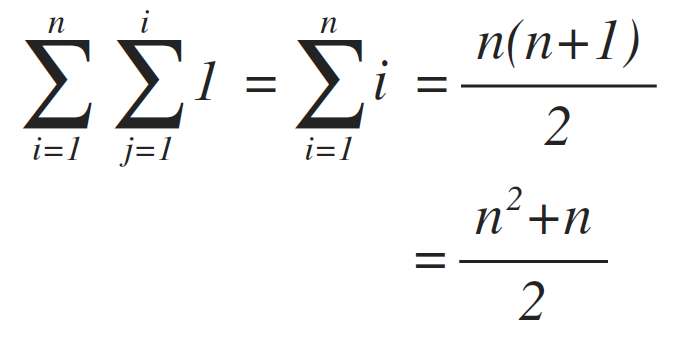
In summary, the execution of each line is every bit follows:
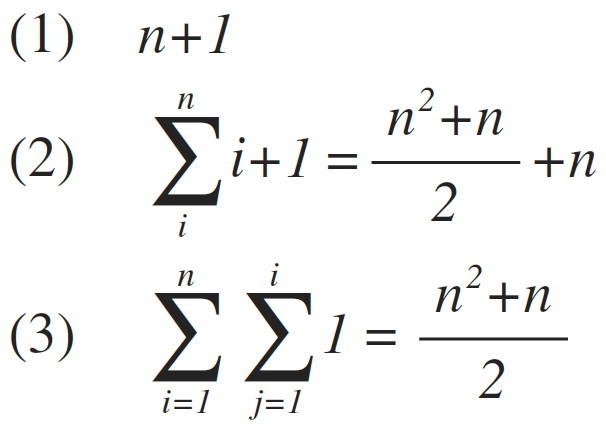
Which yields a sum of:
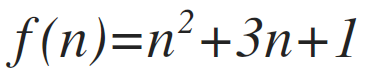
As an gauge, snippet2 will have a worst case operation of:
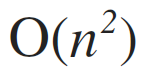
If it's not quite obvious nevertheless, the Large-Oh is merely the largest term in the equation. Yep.
Okay, so far nosotros've covered loops with capricious repetitions n. Now, let's try something concrete and quite simpler…
snippet3: (i) for i <- 1 to 100:
(ii) for j <- one to 50:
(3) print(i,j)
Using the aforementioned technique we used from the previous examples, line (ane) tin be evaluated to execute 100+one times.
Line (two): loop j is evaluated to execute 50+1 times, and repeated 100 times past the outer loop i. Which is: (l+i)(100) = 5100.
Line (3) is evaluated to execute one time, repeated by 50 times by loop j, and 100 times by the loop i. Which is: (1)(50)(100) = 5000.
The sum of the frequency count per line yields: f(n)=10201 total. Since f(n) is a constant, the worst case interpretation is O(one) — besides known as constant time.
Regardless of how large f(northward) is, every bit long as information technology stand for a constant number, will always be written as O(1) to correspond constant time estimation.
How about the combination of something physical and arbitrary?
Okay, here nosotros go! I'll be going fast this time.
snippet4: (1) for i <- 1 to north:
(two) for j <- 1 to 100:
(3) print(i,j)
Line (1) executes n+ane times.
Line (2) executes 100+ane times, repeated by the loop i for n times. Which is: (100+one)(northward)=101n.
Line (3) executes ane time, repeated by the loop j for 100 times and n times by the loop i. Which is: (ane)(100)(n)=100n.
The sum of the frequency count per line yields: 202n+i; with a worst-case estimation of O(n).
We've been going easy for a while.
Did you notice that the loop examples above always starts with 1? What if we modify the lower spring of the i loop of whatsoever number other than 1?
Allow's try and do that.
snippet5: (1) for i <- 4 to due north:
(2) for j <- 1 to north:
(3) print(i,j)
As you lot see, the loop i in line (1) starts at 4. We tin can apply this handy formula to evaluate line (1):
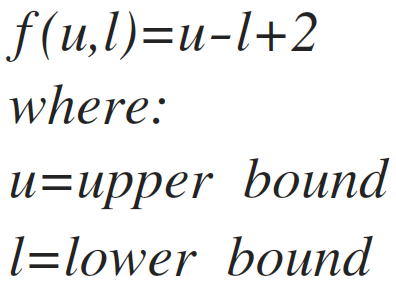
The lower leap of loop i is iv, and the upper spring is n. Using the formula, we can learn the frequency count of line (ane) equally:
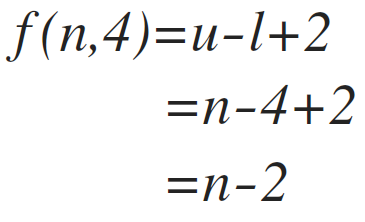
Line (2) is pretty straightforward. The line is executed n+1 times, repeated past north-3 times by the loop i.
Wait, why is the loop j repeated n-iii times, when clearly loop i was formerly evaluated n-2 times prior?
Remember that nosotros have a +1 every bit the loop exit in loop i? If n-2 has included a +1 as an exit, then excluding it to count the number of repetitions inside the loop will yield: north-2-1=n-3.
Going back to line (two), the frequency count is:
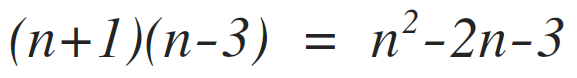
Line 3 is executed i time, repeated northward times past the j loop, and northward-3 times by the i loop. Which is:
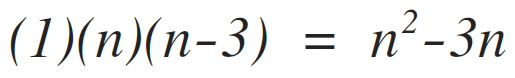
Summing up the frequency count for each line yields:
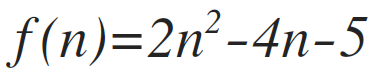
With a worst interpretation of:
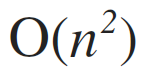
If you're into more adventure, we can also endeavor irresolute the lower spring of the inner loop j.
snippet6: (1) for i <- 1 to 2n
(2) for j <- 5 to i
(three) print(i,j)
Line (1) is simple as you should exist familiar on information technology past now. The line gets executed 2n+one times.
You know where that +1 was from correct? Great.
Line (2) involves a lot of tricks. If you recollect of summations, you lot're correct! But before we use summations, we first need to make up one's mind how many times j repeats itself with respect to i when j's lower bound is five.
Remember the handy formula? Gauge t'was handy after all.
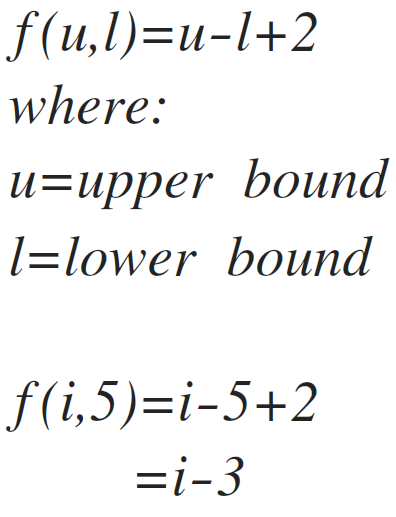
Now, we can't assume i-3 as the frequency count equally i is a variable from 1 to due north. So we need to write the frequency count of line (2) in summation form, which is written as follows:
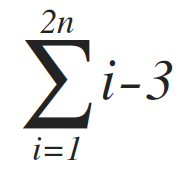
In order to sum information technology later with the rest of the code, we demand to simplify the summation:
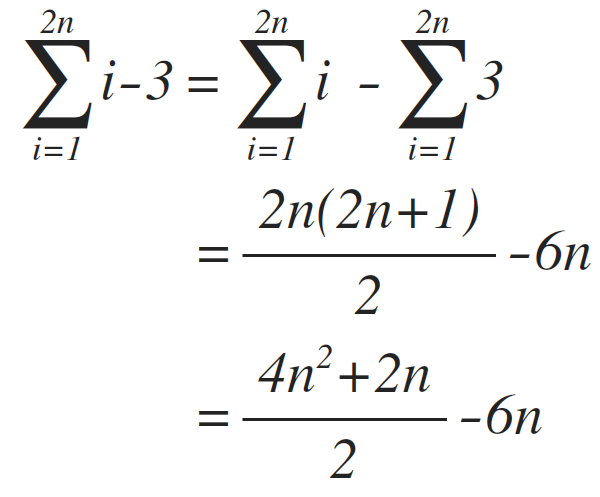
Evaluating line (3) volition be a tad challenging. Line (3) executes 1 fourth dimension, repeated by i-4 times by the inner j loop, and 2n times past the outer i loop. Since j depends on i which is a variable, the frequency count should be written in summation form. Which should exist:
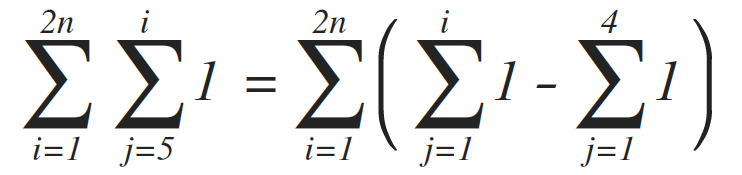
By simplifying the summation, nosotros get:
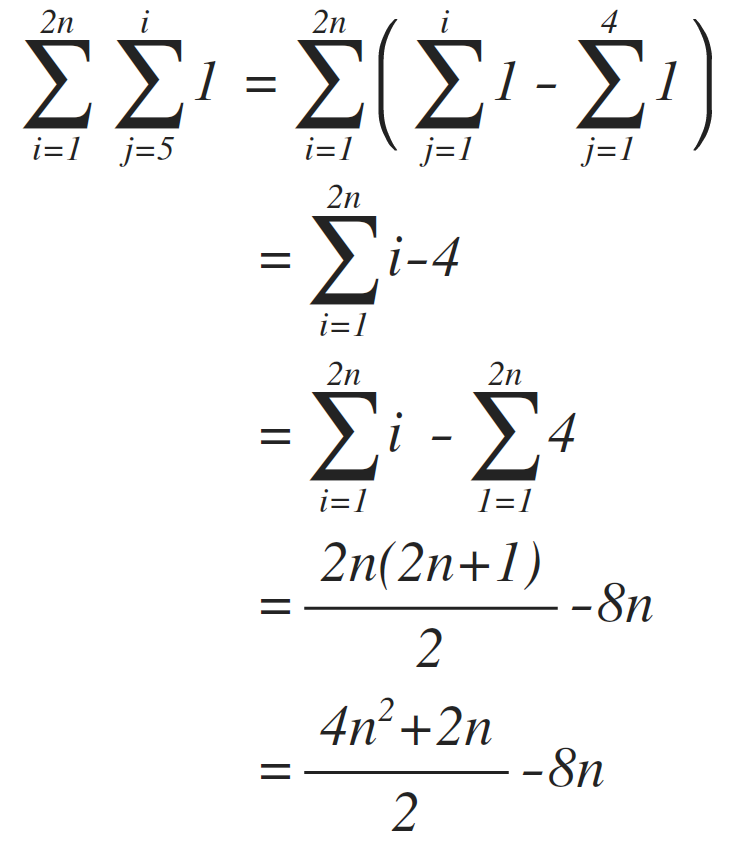
In summary, the execution of each line is as follows:
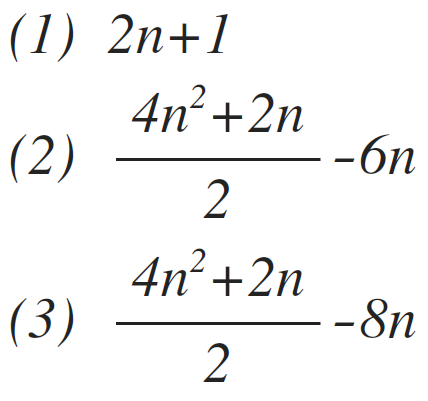
Summing the frequency count of each line yields:
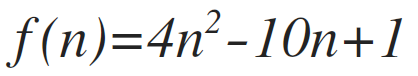
At worst, the code performs:
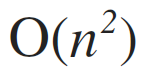
Fascinating, yes?
In part 4 of this series, we will be roofing unlike asymptotic notations such every bit Big-Oh, Big-Omega, Big-Theta, Little-Oh, and Little-Omega. After which, nosotros will explore analysing:
one. Iii-nested loops.
ii. Loops whose lower jump is a variable instead of a constant.
3. Reversed (descending) loops.
And then far, we are discussing analysis on unproblematic iterative algorithms. We will discuss asymptotic notations in part 4, including more examples in loop assay.
Farther, nosotros will tackle how to analyse recursive algorithms that are famous to do dissever and conquer approach (which solves a big problem by breaking it down into smaller, manageable sub-issues).
But afterwards which we can discuss the assay of algorithms which does something similar search and sort.
Until so, have a break, and take a good nap.
A long post deserves a potato.

That's information technology for now!
Cheers!
Source: https://medium.com/@ionarciso/a-priori-analysis-of-algorithms-b6fcbf1319c3
Posted by: polkconat1975.blogspot.com

0 Response to "How To Find Frequency Count Of Algorithm"
Post a Comment